Quelle est la fonction du module Lissage statistique ?
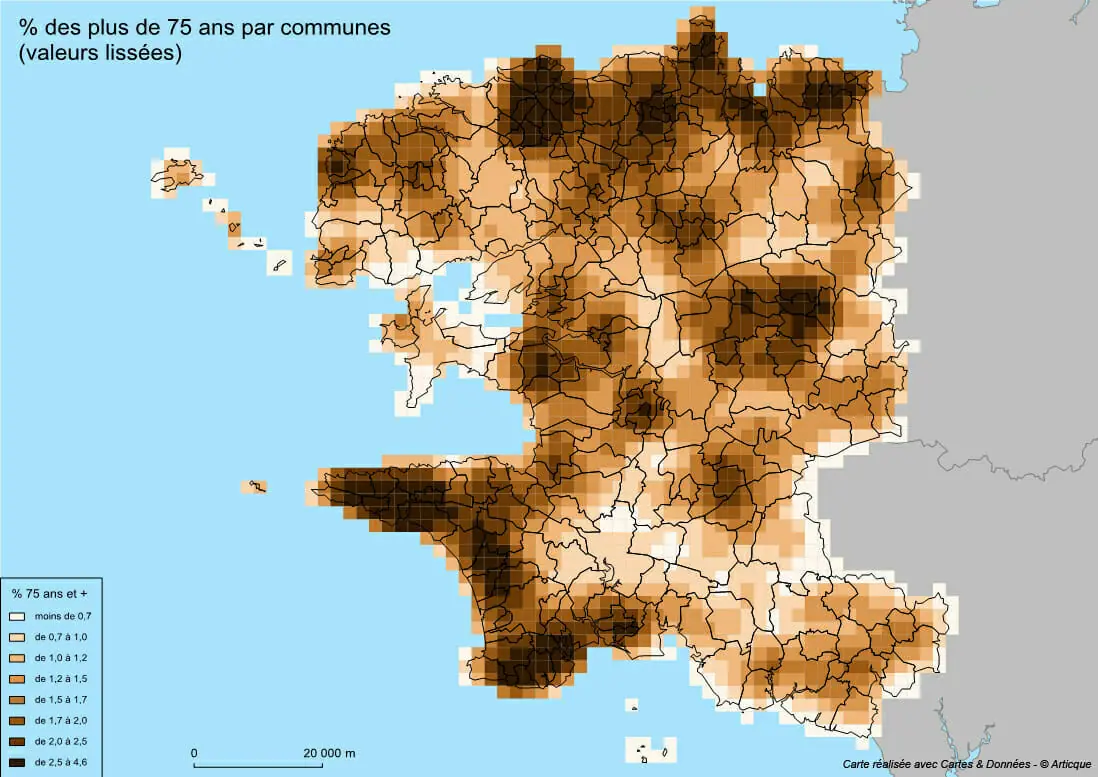
Le module Lissage permet de corriger des valeurs « extrêmes » sur une carte en les relativisant par rapport aux données des territoires qui leur sont proches.
Il permet ainsi de minimiser les disparités sur vos cartes pour mieux mettre en évidence les grandes tendances des phénomènes que vous représentez, les rendant ainsi plus simple à lire et plus « synthétiques ».
Présentation du module Lissage
Le lissage permet dans Cartes & Données de corriger des valeurs chiffrées attribuées aux entités d’un fond de carte en tenant compte de la valeur des entités environnantes.
L’intérêt de cette opération est double, il permet de :
- corriger les valeurs extrêmes éventuellement erronées (erreurs de mesures, etc…)
- faire apparaître les grandes tendances spatiales des variables en « aplatissant » les irrégularités des phénomènes.
Concrètement, le module Lissage va regarder la valeur de chaque entité de la carte, et la corriger en fonction de celles des entités géographiques proches :
- les valeurs fortes vont diminuer pour tenir compte des valeurs faibles proches
- les valeurs faibles vont augmenter pour tenir compte des valeurs fortes proches
Lisser des données, c’est admettre qu’un phénomène étudié prend des valeurs qui diffèrent progressivement au fur à mesure que l’on s’éloigne d’un point donné. Dans sa version la plus simple, le lissage ne prend pas en compte des obstacles naturels ou un réseau routier par exemple. Il doit donc être utilisé avec prudence dans des régions montagneuses ou à une échelle assez fine. Au niveau infra-communal, la notion de frontière peut s’avérer importante : la continuité n’est donc pas garantie.
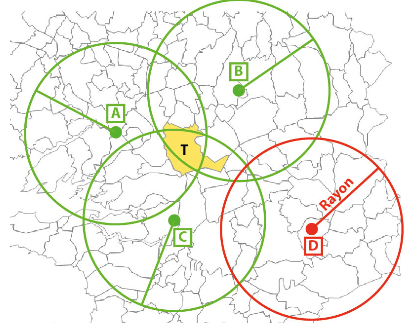
Le rayon de lissage
Le lissage remplace le comptage de valeur pour chaque territoire (sa valeur actuelle) par un comptage dans un voisinage. Ce voisinage est défini par un rayon, c’est à dire une distance autour de chaque territoire dans laquelle celui-ci va « compter » les différentes valeurs voisines pour corriger la sienne.
Le rayon est donc une valeur de distance exprimée dans l’unité des coordonnées de votre document de travail (m, km, etc.).
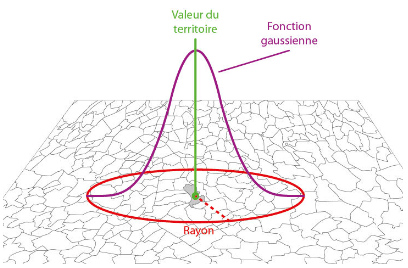
La fonction de lissage
Cette fonction est la méthode de comptage dans un voisinage utilisée pour lisser la valeur de chacun des territoires.
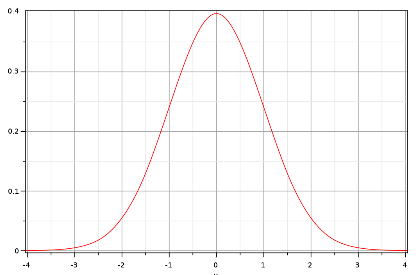
La fonction gaussienne
La fonction gaussienne est la plus étendue et la plus utilisée.
C’est une courbe en cloche dont l’axe de symétrie est l’ordonnée d’un repère orthonormé. Cette méthode de lissage induit donc une distribution symétrique à partir d’un point (l’ordonnée du graphique qui est le point d’un territoire ou le centroïde d’un polygone).
Spatialement, plus on s’éloigne du point, plus le poids de la valeur de ce point diminue en suivant le profil de la courbe de Gauss : la diminution n’est donc pas linéaire. Elle dépend en réalité du rayon de lissage : plus il est petit, plus le poids d’un point diminue rapidement, et inversement.
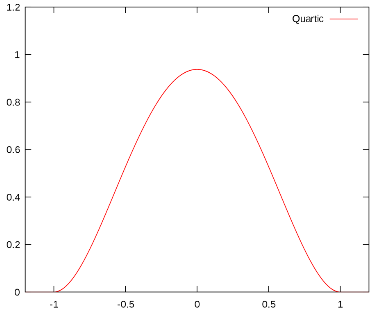
La fonction quartique
La fonction quartique ressemble beaucoup à la fonction gaussienne, mais la décroissance du poids des valeurs des territoires en fonction de l’éloignement est beaucoup plus graduelle.
C’est une courbe en cloche dont l’axe de symétrie est l’ordonnée d’un repère orthonormé. Cette méthode induit donc une distribution symétrique à partir d’un point (l’ordonnée du graphique qui est le point d’un territoire ou le centroïde d’un polygone).
Spatialement, plus on s’éloigne du point, plus le poids de la valeur de ce point diminue en suivant le profil de la courbe de Gauss : la diminution n’est donc pas linéaire. Elle dépend en réalité du rayon de lissage : plus il est petit, plus le poids d’un point diminue rapidement, et inversement.
Lien entre le rayon et la fonction
Le rayon de lissage et la fonction utilisée sont très liés. Le rayon influe non seulement sur les territoires qui seront exclus/pris en compte dans les calculs, mais aussi sur la fonction de lissage. En d’autres termes, plus le rayon de lissage sera faible plus la courbe du graphique aura une pente importante.
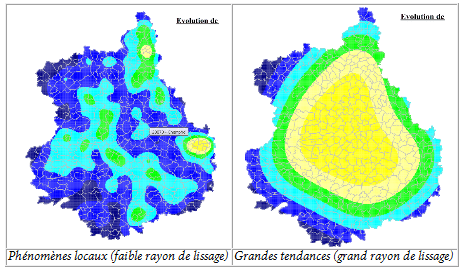
La valeur du rayon lissage est à déterminer de façon rigoureuse en fonction des données et de la répartition spatiale des objets. La taille du rayon de lissage dépendra de la répartition spatiale de l’échantillon. Pour conclure, un faible rayon de lissage mettra en valeur les phénomènes locaux et un fort rayon montrera les grandes tendances spatiales.
Exemple de variation de la fonction gaussienne selon différents rayons de lissage
Quel est le résultat observé ?
Le module Lissage génère une nouvelle donnée continue, qui correspond aux valeurs lissées des entités géographiques étudiées.
Articque est le pionnier français de la prise de décision stratégique grâce à la cartographie. Editeur de solutions géodécisionnelles depuis plus de 30 ans, nous aidons les organismes et entreprises à mieux piloter leurs activités et à éclairer leurs décisions. Elles gagnent ainsi en performance grâce à une connaissance approfondie de leur territoire.
ARTICQUE - TOURS,
149 avenue du Général de Gaulle,
37230 Fondettes – France
02 47 49 90 49
